publications
publications by categories in reversed chronological order.
2024
- GPA
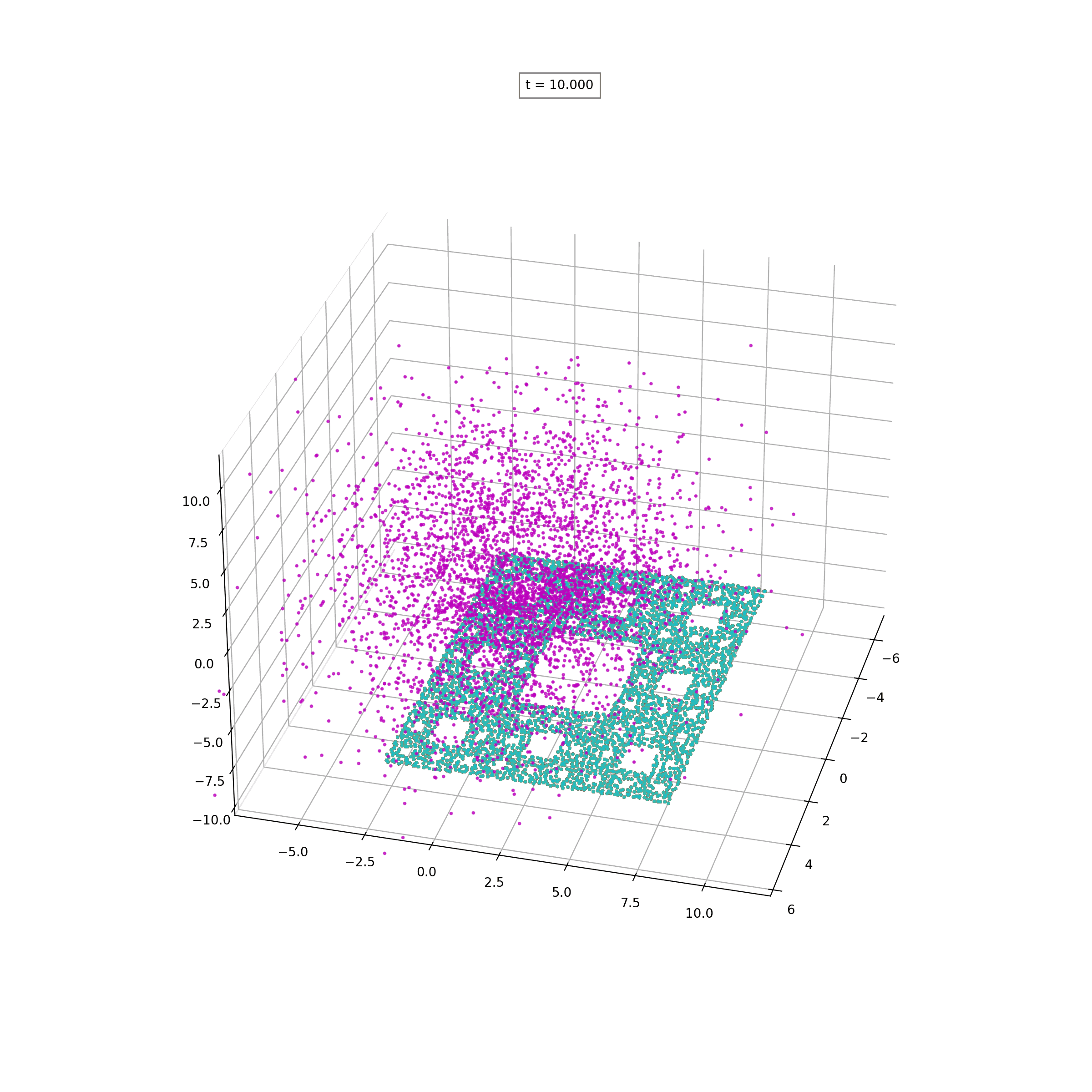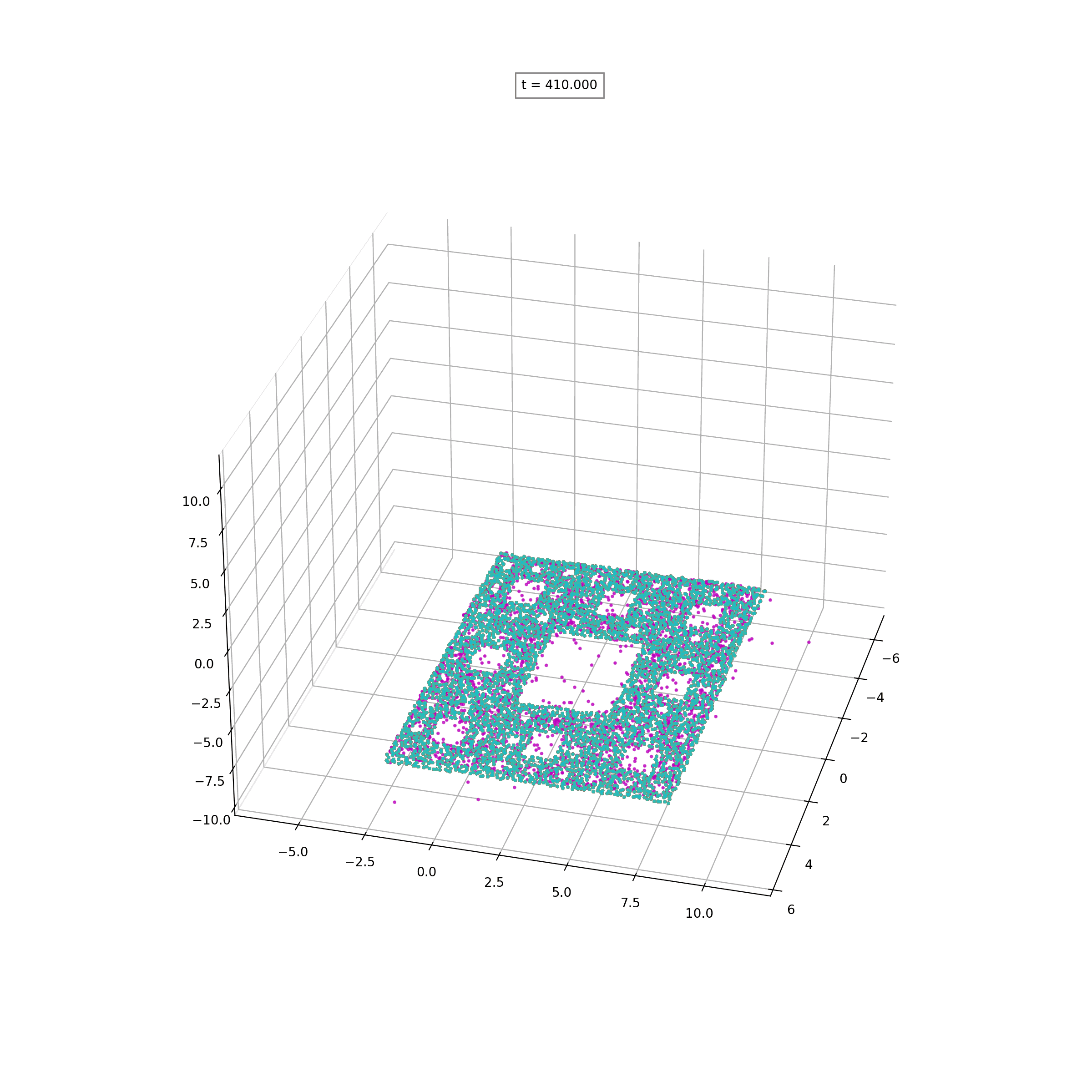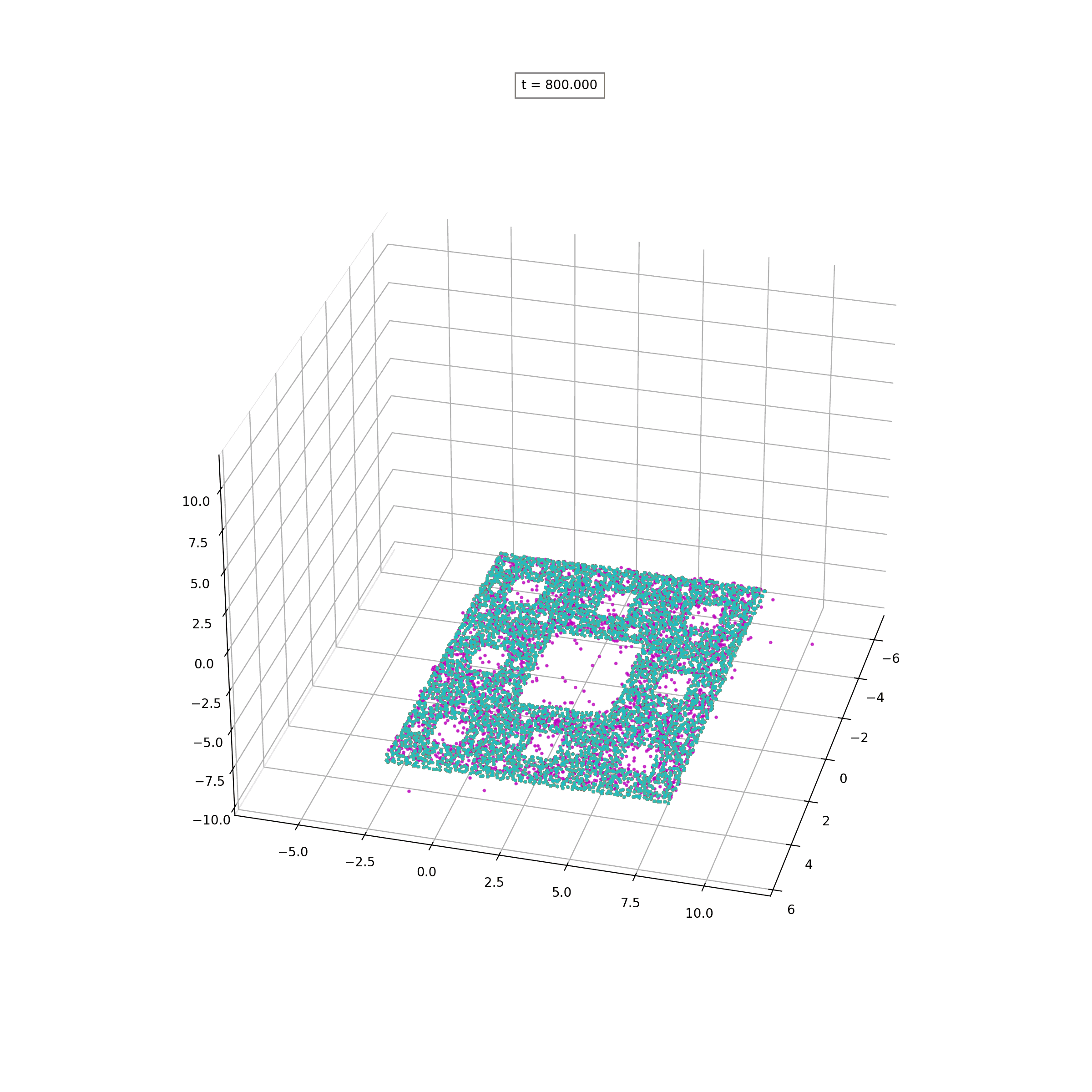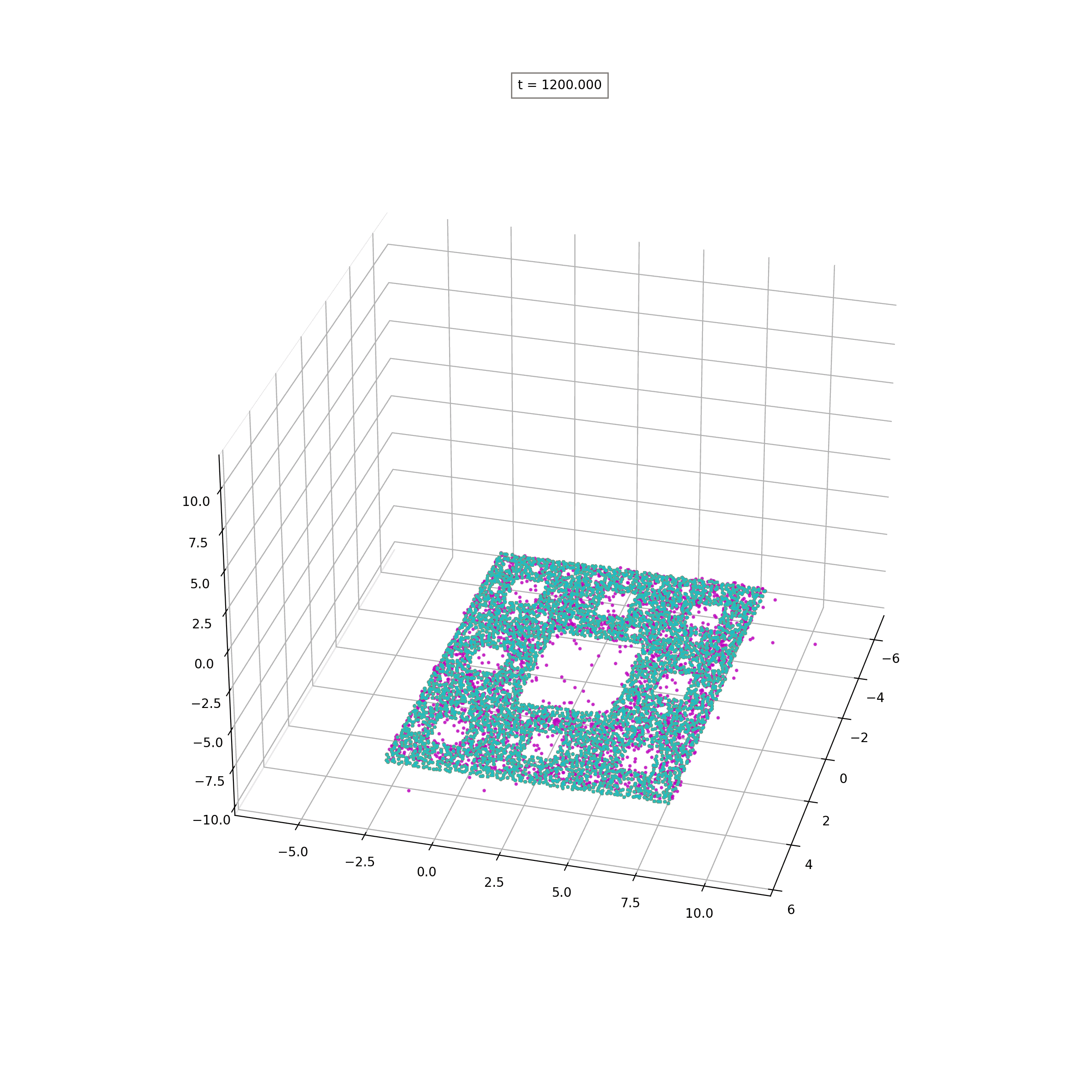 Lipschitz-Regularized Gradient Flows and Generative Particle Algorithms for High-Dimensional Scarce DataSIAM J.Data Science, to appear, 2024
Lipschitz-Regularized Gradient Flows and Generative Particle Algorithms for High-Dimensional Scarce DataSIAM J.Data Science, to appear, 2024 - W-ProximalsCombining Wasserstein-1 and Wasserstein-2 proximals: robust manifold learning via well-posed generative flows2024
- Heavytail-W-ProximalsLearning heavy-tailed distributions with Wasserstein-proximal-regularized α-divergences2024