RA ch10 Diagnostics
Ch 10: Diagnostics
Once we’ve established a model, the next step is to try to improve the model. Or if the model is stuck in a trouble, we should diagnose in which part the trouble comes. In linear regression model, the possible reasons would be
- improper functional form of a predictor variable
- outliers
- influential observations
- multicollinearity.
Here are some suggestions for detecting such factors.
Outline
- Model adequacy for a predictor variable
- Outliers and influential cases
- definitions
- identifying high leverage observations
- identifying outliers
- identifying influential cases
- Multicollinearity diagnostic
1. Model adequacy for a predictor variable
You draw added-variable plots to detect if there is an improper functional form of a predictor variable. For a regression model with 2 predictor variables \(X_1\) and \(X_2\), we want to find the regression effect for \(X_1\) given that \(X_2\) is already in the model. Here are the steps.
-
Regress \(Y\) on \(X_2\) and obtain
fitted values with \(X_2\) data, \(\hat{Y_i}(X_2) = b_0 + b_1 X_{i2}\) and
its residuals, $$e_i(YX_2) = Y_i - \hat{Y_i}(X_2)$$. -
Regress \(X_1\)(testing variable) on \(X_2\) and obtain
fitted values with \(X_2\) data, \(\hat{X_{i1}}(X_2) = b_0^\ast + b_1^\ast X_{i2}\) and
its residuals, $$e_i(X_{i1}X_2) = X_{i1} - \hat{X_{i1}}(X_2)$$. - Draw added an added-variable plot (X-axis: \(e_i(X_{i1}\mid X_2)\), Y-axis: \(e_i(Y \mid X_2)\))
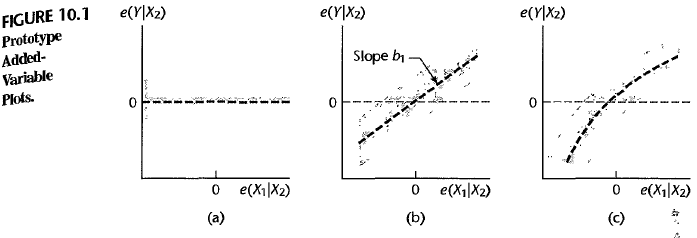
a. No additional information exists from adding $$X_1$$.
b. There is additional linear information from adding $$X_1$$.
c. There is additional nonlinear information from adding $$X_1$$.
2. Outliers and influential cases
definitions
- An outlier is an observation whose response \(Y\) is far from the rest of the observations.
- An observation has high leverage if it has “extreme” predictor \(X\) values which is distant from other \(X\) values. ex) one-variable case: An extreme \(X\) value is simply one that is particularly high or low. ex) multiple-variables case: Extreme \(X\) values may be particularly high or low for one or more predictors, or may be “unusual” combinations of predictor values.
- A data point is influential if it influences excessively in making a regression model. It can influence in the predicted responses, the estimated slope coefficients, or the hypothesis test results. Outliers and high leverage observations are likely to be influential.
When it comes to a model with one-predictor variable, we can simply look at scatter plots in order to identify any outliers and high leverage observations.
What if we have a model with multiple predictor variables? We can identify such observations by diagonal entries of the hat matrix \(H = X(X^tX)^{-1}X^t\).
- We name \(h_{ii}\) as leverage value. Leverage values can be calculated by \(h_{ii} = X_i^t (X^tX)^{-1}X_i\).
identifying high leverage observations
\(h_{ii}\) has useful properties such as
- \[0 \leq h_{ii} \leq 1\]
- \[\sum_i h_{ii} = rank(H) = p\]
- \[Var(e_i) = (1-h_{ii})\sigma^2\]
By property 2, (mean of \(h_{ii}\)) = \(\frac{p}{n}\). Also, by property 3, we can see that if \(h_{ii}\) is large, then the observed response \(Y_i\) plays a large role in the value of the predicted response \(\hat{Y_i}\). \(\Rightarrow\) if \(h_{ii}\) is twice larger than the average (\(h_{ii}>\frac{2p}{n}\)), then such case is a high leverage observation.
identifying outliers
Recall We have used studentized residual \(r_i = \frac{e_i}{s^2(e_i)} = \frac{e_i}{\sqrt{MSE(1-h_{ii})}} \sim t(n-p)\) to identify unusual \(Y\) values. But this approach can have a risk. That is, a potential outlier pulled the estimated regression function toward them, so that it is not flagged as an outlier using the standardized residual criterion.
To address this issue, we use an alternative criterion using studentized residuals. We delete an observation \(Y_i\) and fit a regression model \(\hat{Y_{(i)}}\) on the remaining \(n–1\) observations. Then, we compare the observed response value \(Y_i\) to their fitted value from \(\hat{Y_{(i)}}\). This produces deleted residuals \(d_i = Y_i - \hat{Y_{i(i)}}\). Standardizing the deleted residuals produces studentized residuals.
We can prove that \(d_i = Y_i - \hat{Y_{i(i)}} = \frac{e_i}{1-h_{ii}}\) proof where \(s^2(d_i) = MSE_{(i)}\left(1 + X_{(i)}^t(X_{(i)}^tX_{(i)})^{-1}X_{(i)} \right) = \frac{MSE_{(i)}}{1-h_{ii}}\). Moreover, we can obtain \(MSE_{(i)}\) using \(MSE\) by the formula \((n-p)MSE = (n-p-1)MSE_{(i)} + \frac{e_i^2}{1-h_{ii}}\). Therefore, \(MSE_{(i)} = \frac{1}{n-p-1} \left((n-p)MSE - \frac{e_i^2}{1-h_{ii}} \right) = MSE + \frac{1}{n-p-1} \left(MSE - \frac{e_i^2}{1-h_{ii}}\right)\).
Thanks to these efforts, we don’t need to fit \(n\) distinct regression lines. And we test for this alternative standardized residual \(t_i = \frac{d_i}{s(d_i)} \sim t(n-p-1)\). If \(\mid t \mid\) is large (from large \(h_{ii}\)), we can conclude that following observation \(Y_i\) is an outlier.
identifying influential cases
DFFITS : Influence of the observation \(Y_i\) on the \(i\)th fitted value \(\hat{Y_i}\)
\[DFFITS_i = \frac{\hat{Y_i} - \hat{Y_{i(i)}}}{\sqrt{MSE_{(i)} h_{ii}}} = t_i \left( \frac{h_{ii}}{1-h_{ii}} \right)^\frac{1}{2}\]If it is larger than 1 (for small to medium sized datasets) and larger than \(2\sqrt{\frac{p}{n}}\) (for large datasets), then \(i\)th case is said to be influential.
Cook’s distance : Influence of the observation \(Y_i\) on the fitted function \(\hat{Y}\)
\[D_i = \frac{\sum_{j=1}^n (\hat{Y_j} - \hat{Y_{j(i)}})^2}{p \cdot MSE} = \frac{e_i^2}{p \cdot MSE} \frac{h_{ii}}{(1-h_{ii})^2} = \frac{1}{p}t_i^2\frac{h_{ii}}{1-h_{ii}}\]If \(D_i\) is 50\% or more, then \(i\)th case is said to be influential.
DFBETAS : Influence of the observation \(Y_i\) on the regression coefficients
\[DFBETAS_{k(i)} = \frac{b_k - b_{k(i)}}{\sqrt{MSE_{(i)} C_{kk}}}, k=0,1,\cdots, p-1\]where \(C_{kk}\) is the \(k\)th diagonal element of \((X^tX)^{-1}\). Note that \(C_{kk} = \frac{\sigma^2(b_k)}{\sigma^2}\). If its absolute value is large, the \(i\) th case is said to be influential.
3. Multicollinearity diagnostic
From a standardized regression model, we obtained correlation matrix \(r_{XX} = x^tx\). Now, we have variance-covariance matrix of standardized regression coefficients \(\sigma^2(b^\ast) = (\sigma^\ast)^2 r_{XX}^{-1}\).
This is the standardized version of \(\sigma^2(b) = \sigma^2 (X^tX)^{-1}\).
Let us define the \(k\)th variance inflation factor \(VIF_k\) as the \(k\)th diagonal element of \(r_{XX}^{-1}\). We can find that \(\sigma^2(b_k^\ast) = (\sigma^\ast)^2 VIF_k\).
\(VIF_k \geq 1\), and we can diagnose multicollinearity among predictor variables by its magnitude.
- If \(VIF_k = 1\), then \(X_k\) is not linearly related to other predictor variables.
- If \(VIF_k \gg 1\), then \(X_k\) has inter-correlation with other predictor variables.
- If \(VIF_k = \infty\), then \(X_k\) is perfectly linearly associated with other predictor variables.
If \(VIF_k \gg 10\) or \(\overline{VIF}= \frac{\sum_{k=1}^{p-1} VIF_k}{p-1}\) is considerably larger than 1, we can say that \(k\)th predictor variable or the entire model has multicollinearity.
Enjoy Reading This Article?
Here are some more articles you might like to read next: