Hyemin Gu

I do research on machine learning founded by mathematics. Working with advisor Markos Katsoulakis, and Luc Rey-Bellet, Yannis Pantazis and Panagiota Birmpa, my recent research is focused on developing particle transportation based generative model which outperforms in a low training data regime. Our approach is to transport particles through gradient flows which minimize regularized f-divergences. We proposed a stable model by applying Lipschitz regularization on a discriminator (as in GANs), and then solving an ODE induced by the gradient of the discriminator. Currently we are focusing on improving the accuracy of solutions by more sophisticated optimization methods, ODE solvers, and so on.

Personally, the following quote influenced my perspective as a researcher. In this sense, I find myself close to Eros described in Symposium.

No one who is wise desires to be wise, for he is so already. Nor do the ignorant desire wisdom: ignorance is satisfied with itself, since one does not desire what he does not suppose he lacks. Those who love wisdom are intermediate between knowledge and ignorance, and Eros is of this nature. Socrates’ speech in Symposium by Pluto

news

Sep 5, 2022	Initiated a role as a TWIGS coordinator.
Jan 12, 2022	Initiated a role as a research assistant, advised by Markos Katsoulakis.

selected publications

GPA

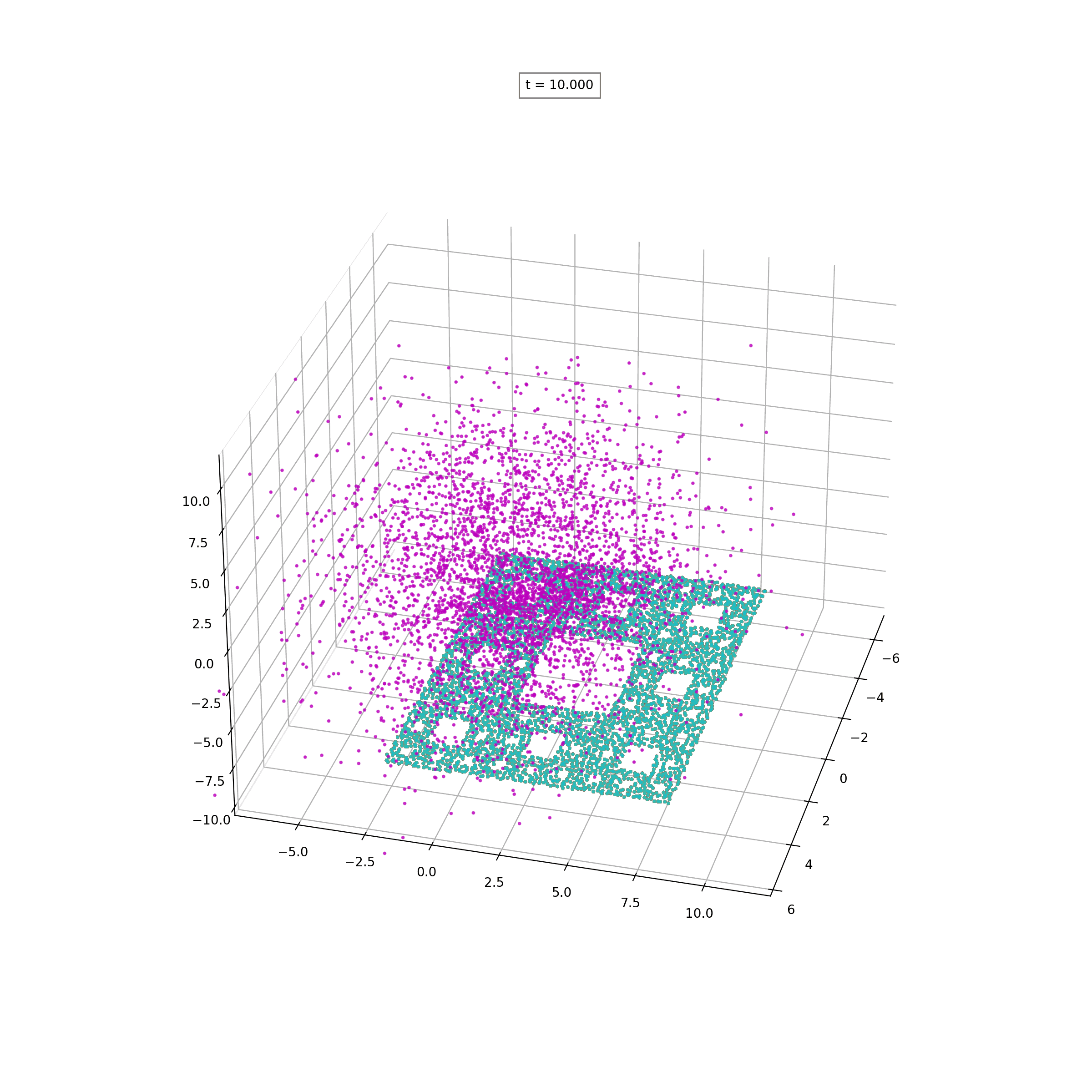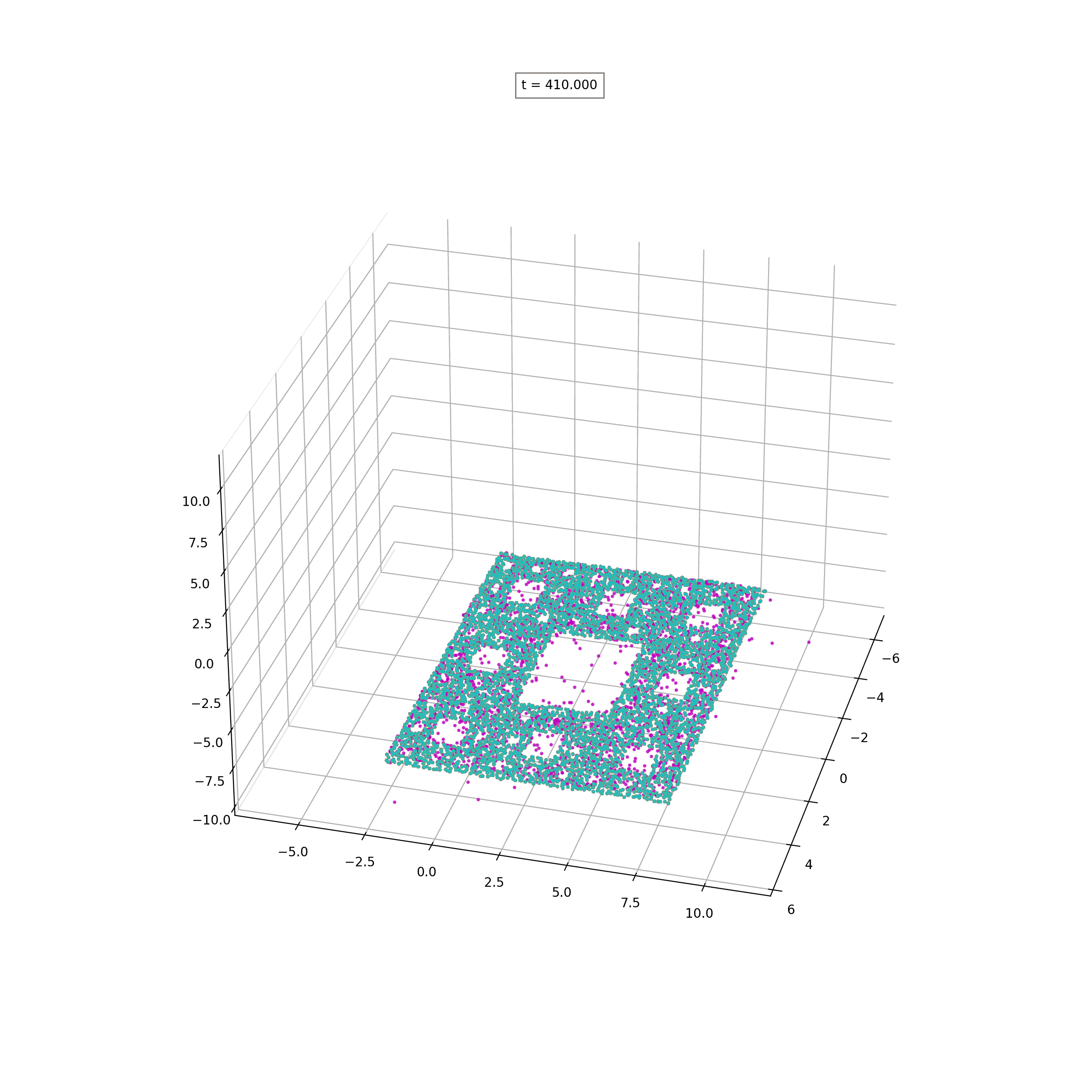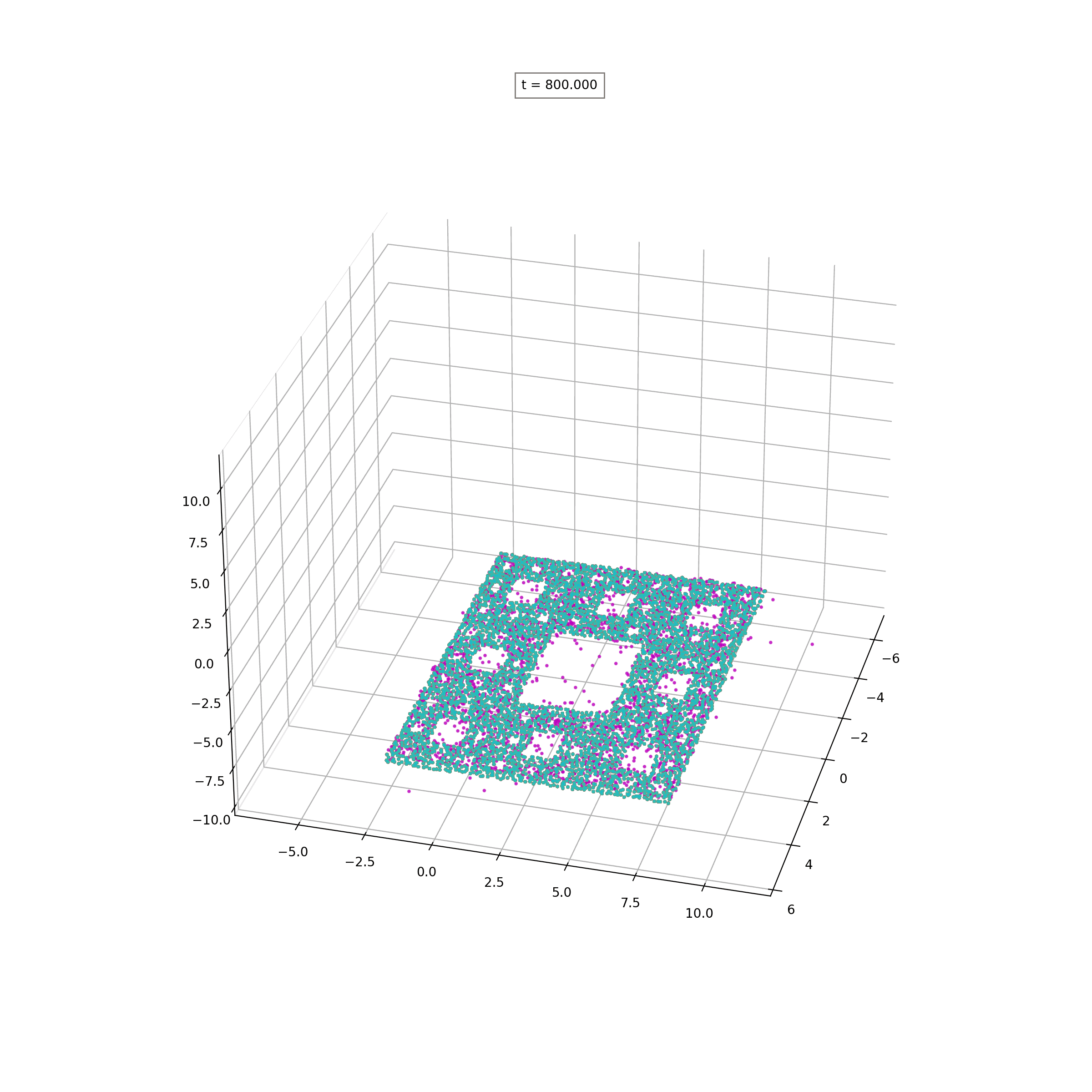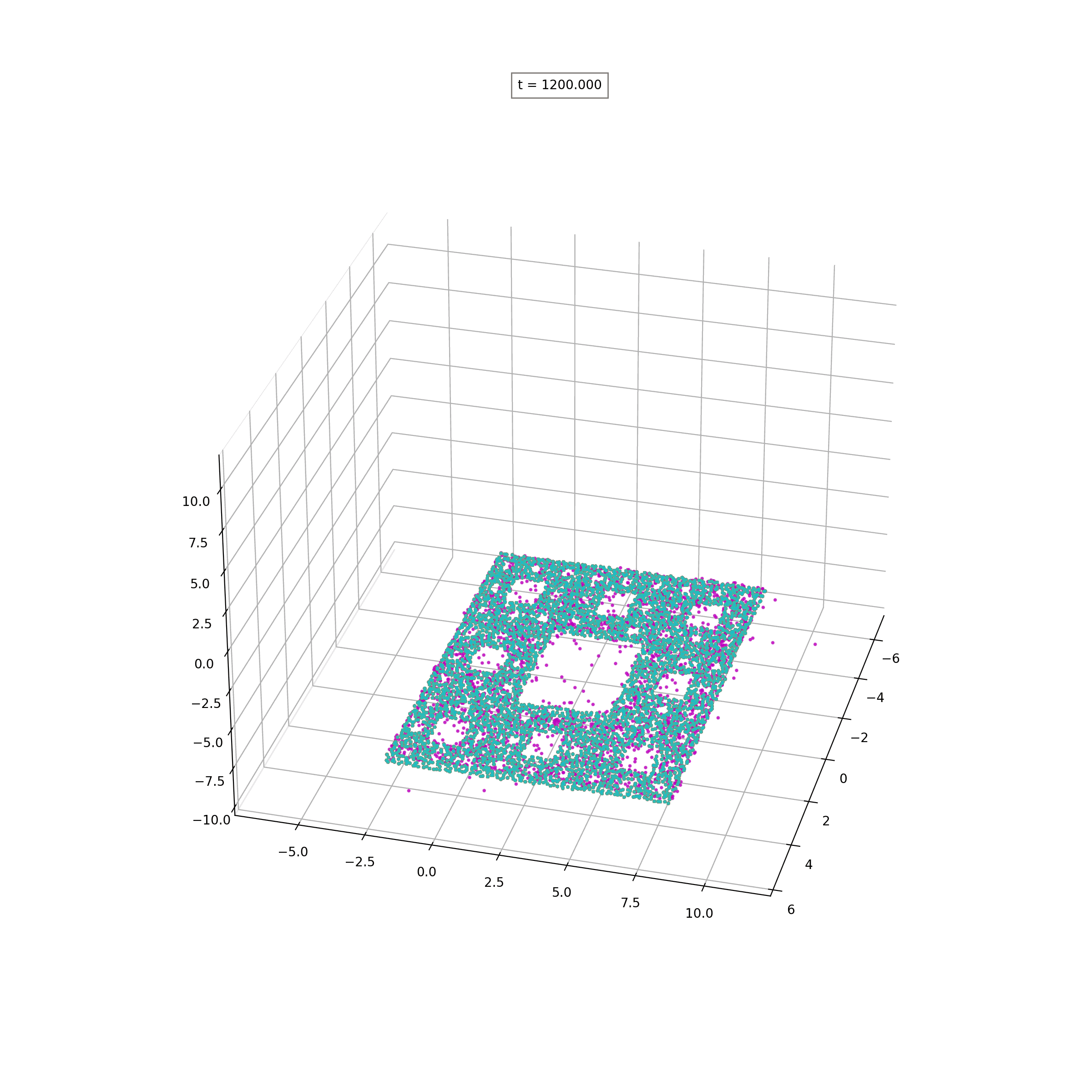Lipschitz regularized gradient flows and latent generative particles

Hyemin Gu, Panagiota Birmpa, Yannis Pantazis, Luc Rey-Bellet, and Markos A. Katsoulakis

2022

Abs

Lipschitz regularized f-divergences are constructed by imposing a bound on the Lipschitz constant of the discriminator in the variational representation. They interpolate between the Wasserstein metric and f-divergences and provide a flexible family of loss functions for non-absolutely continuous (e.g. empirical) distributions, possibly with heavy tails. We construct Lipschitz regularized gradient flows on the space of probability measures based on these divergences. Examples of such gradient flows are Lipschitz regularized Fokker-Planck and porous medium partial differential equations (PDEs) for the Kullback-Leibler and alpha-divergences, respectively. The regularization corresponds to imposing a Courant-Friedrichs-Lewy numerical stability condition on the PDEs. For empirical measures, the Lipschitz regularization on gradient flows induces a numerically stable transporter/discriminator particle algorithm, where the generative particles are transported along the gradient of the discriminator. The gradient structure leads to a regularized Fisher information (particle kinetic energy) used to track the convergence of the algorithm. The Lipschitz regularized discriminator can be implemented via neural network spectral normalization and the particle algorithm generates approximate samples from possibly high-dimensional distributions known only from data. Notably, our particle algorithm can generate synthetic data even in small sample size regimes. A new data processing inequality for the regularized divergence allows us to combine our particle algorithm with representation learning, e.g. autoencoder architectures. The resulting algorithm yields markedly improved generative properties in terms of efficiency and quality of the synthetic samples. From a statistical mechanics perspective the encoding can be interpreted dynamically as learning a better mobility for the generative particles.